REx established new state-of-the-arts in three challenging code generation domains.
Iteratively improving and repairing source code with large language models (LLMs), known as refinement, has emerged as a popular way of generating programs that would be too complex to construct in one shot. Given a bank of test cases, together with a candidate program, an LLM can improve that program by being prompted with failed test cases. But it remains an open question how to best iteratively refine code, with prior work employing simple greedy or breadth-first strategies. We show here that refinement exposes an explore-exploit tradeoff: exploit by refining the program that passes the most test cases, or explore by refining a lesser considered program. We frame this as an arm-acquiring bandit problem, which we solve with Thompson Sampling. The resulting LLM-based program synthesis algorithm is broadly applicable: Across loop invariant synthesis, visual reasoning puzzles, and competition programming problems, we find that our new method can solve more problems using fewer language model calls.
Using large language models (LLMs) to generate code has become increasingly popular for enhancing programmer productivity and building automated agents. With LLMs, users can simply describe their requirements in natural language, and the models generate code to match those specifications. However, LLMs do not always get the correct solution right away. Users may need to guide the model further, asking it to either debug the code based on specific errors or abandon the current attempt and regenerate the code altogether.
Consider a typical example of code generation with an LLM:
User Prompt: Your task is to calculate a^b mod 1337. Please write a Python program to do it.
Machine Response: Sure, here is the code:def powmod(a, b): return math.pow(a, b) % 1337.
User Prompt: The code you provided is incorrect. Here is the error message:OverflowError: math range error. Please fix it.
Machine Response: I see. Let me try again. Here is the updated code:def powmod(a, b): return a ** b % 1337.
The entire process of LLM-based code generation and refinement can be visualized as building a refinement search tree. Each node in this tree represents a code version, and each refinement by the LLM adds a new child node. Because LLMs are inherently probabilistic and can produce a wide range of potential solutions, each node could theoretically have an unlimited number of children. Additionally, users can request refinements iteratively, making this search tree infinitely broad and deep.
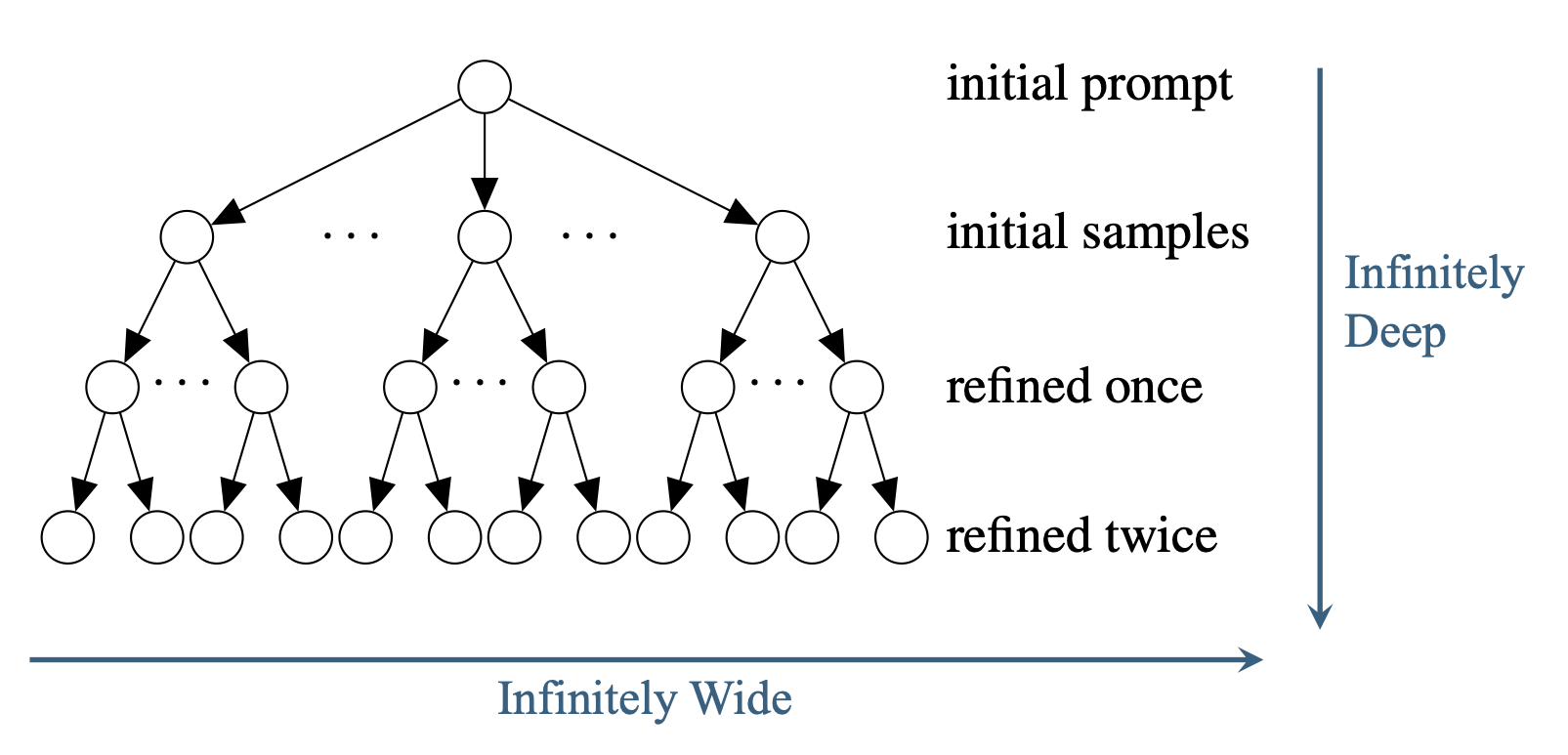
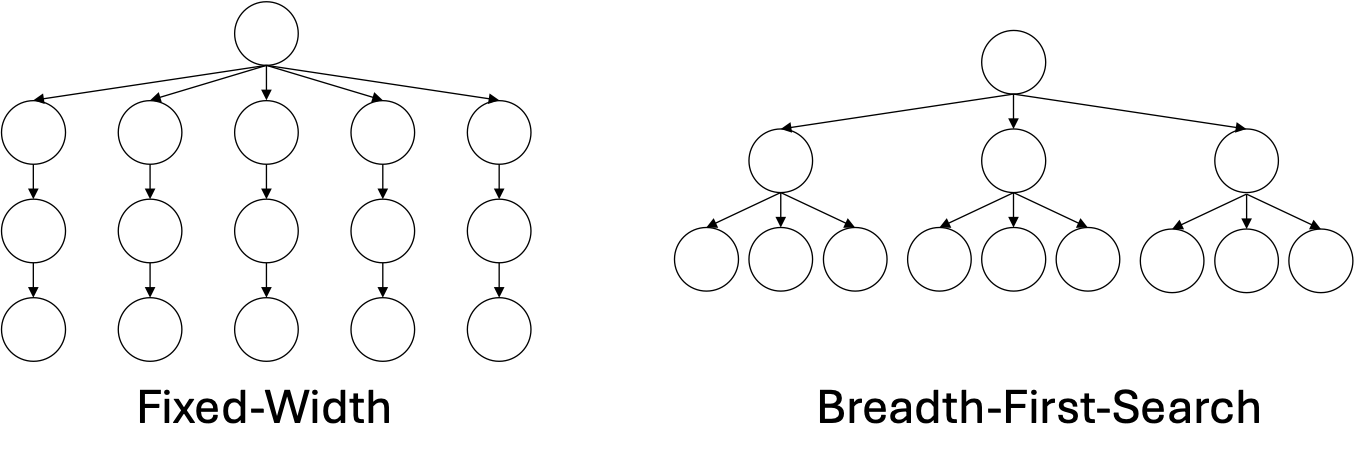
Previous methods have approached code refinement by expanding the tree using fixed strategies like Breadth-First Search (BFS) or Fixed-Width (FW), but these methods are inefficient. It often takes hundreds or even thousands of LLM queries to solve practical programming tasks, which is both costly and time-consuming. Moreover, there is no clear way to choose the optimal strategy or hyperparameters beforehand, and these fixed approaches often lack robustness across different domains and models.
Instead of relying on static, blind exploration strategies like traditional methods, we introduce REx, a smarter and more flexible way to adaptively expand the refinement tree. REx dynamically chooses which code to refine, leading to a more efficient search process. The REx algorithm has set new state-of-the-art results across three diverse domains, demonstrating its robustness and generalizability across different types of tasks and LLMs. Moreover, it is straightforward to implement with just a few lines of code, and it saves 10-80% of LLM requests compared to baseline methods, depending on the domain.
REx is inspired by two simple principles drawn from human programming experience:
Focus on Promising Code: Some code versions are closer to being correct than others, so it makes sense to prioritize refining those first.
Avoid Over-Focusing: If a particular code has been refined too many times without success, it is better to move on and explore other possibilities.
Consider a simple refinement tree where the agent decides to regenerate twice, resulting in two versions of code. One version passes 80% of the test cases, while the other passes 60%. As a smart human agent, what would you do? Would you refine the 80% accurate code, the 60% accurate one, or regenerate from scratch? Assuming the pass rate on test cases is a reasonable heuristic for code quality, it makes sense to refine the 80% accurate code first.
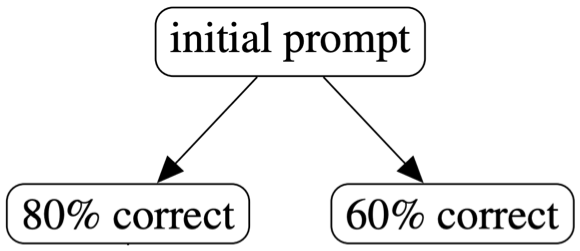
Now, suppose the refined version of the 80% code ends up with 0% accuracy. What would you do next? Would you continue refining the 80%, the 60%, the 0%, or regenerate? It is likely that you are now less inclined to continue refining the 80% accurate code.
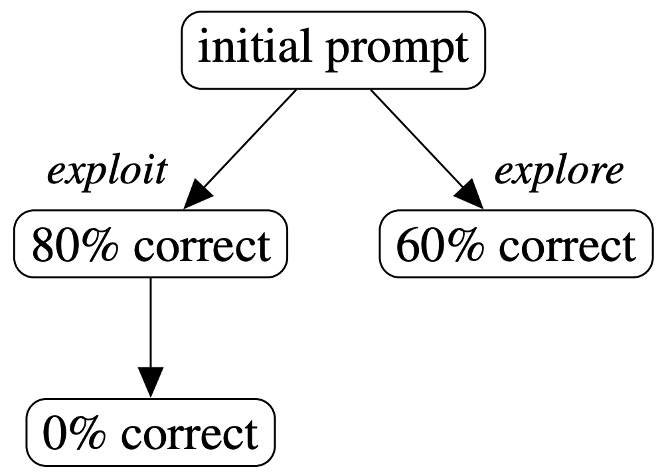
This scenario illustrates the exploration-exploitation dilemma in expanding the refinement tree. Initially, it makes sense to focus on refining the better-performing codes. However, if refining one code fails too many times, it is wiser to explore other less-refined options.
To properly balance the exploration-exploitation tradeoff, we frame the refinement tree expansion problem as a bandits problem and incorporate a bandits algorithm, Thompson Sampling, to solve it. Concretely, each arm/action corresponds to refining each code. The reward is whether the refinement succeeds. It's easy to incorporate heuristic values such as pass rates as the prior in Thompson Sampling. At each step of the REx algorithm, it decides which code to refine by sampling the beta distributions:
def REx(problem, C):
programs = {problem.empty_solution()}
failed_cnt = defaultdict(lambda: 0) # Nρ in paper
while True:
program = max(programs, key=lambda p: np.beta(
1 + C*p.heuristic_value, # 1 + C × h(ρ)
1 + C*(1-p.heuristic_value)+failed_cnt[p] # 1 + C × (1 − h(ρ)) + Nρ
))
new_program = program.refine(problem) # ρ′ ∼ Prefine(·|ρ, Φ)
if is_solved(problem, new_program): # ρ′ ⊢ Φ in paper
return new_program
failed_cnt[program] += 1
programs.add(new_program)
We systematically evaluate REx in three diverse challenging code generation tasks: loop invariant synthesis, visual reasoning puzzles, and competition programming problems. We also exvaluate REx with four different LLMs: GPT-4, GPT-3.5-turbo, Claude-3.5-Sonnet, and Llama-3.1-405B. REx outperforms the baselines in all three tasks and across all four LLMs, demonstrating its robustness and generalizability.
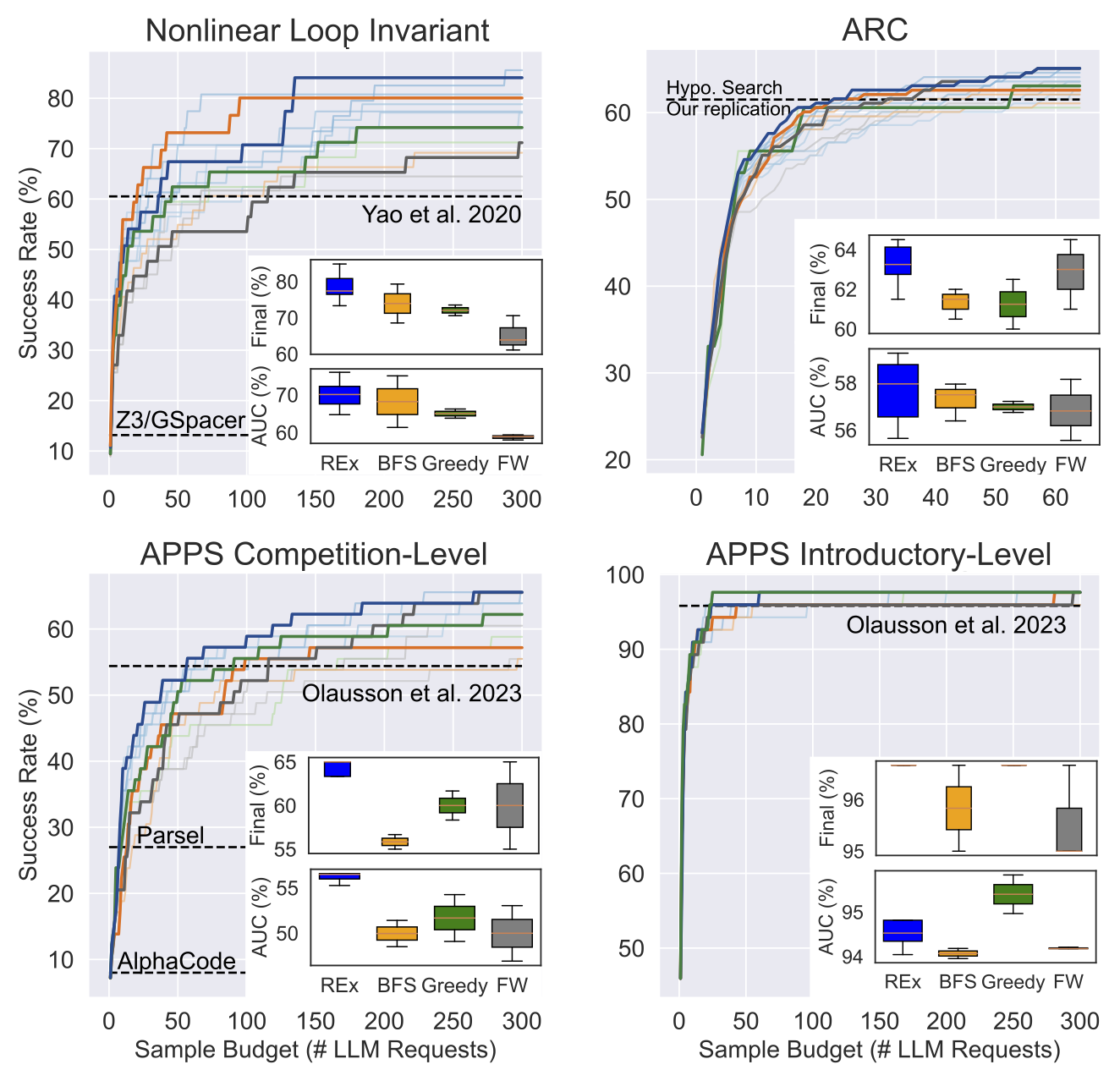As shown in the above figure, REx established new SOTAs and consistently outperforms the baselines across three diverse domains: loop invariant synthesis, visual reasoning puzzles, and competition programming problems. Dark lines show performance with the best hyper-parameter setting for each method. Light lines show each run on each hyperparameter. The inset box plots show the distribution while varying the hyper-parameters.
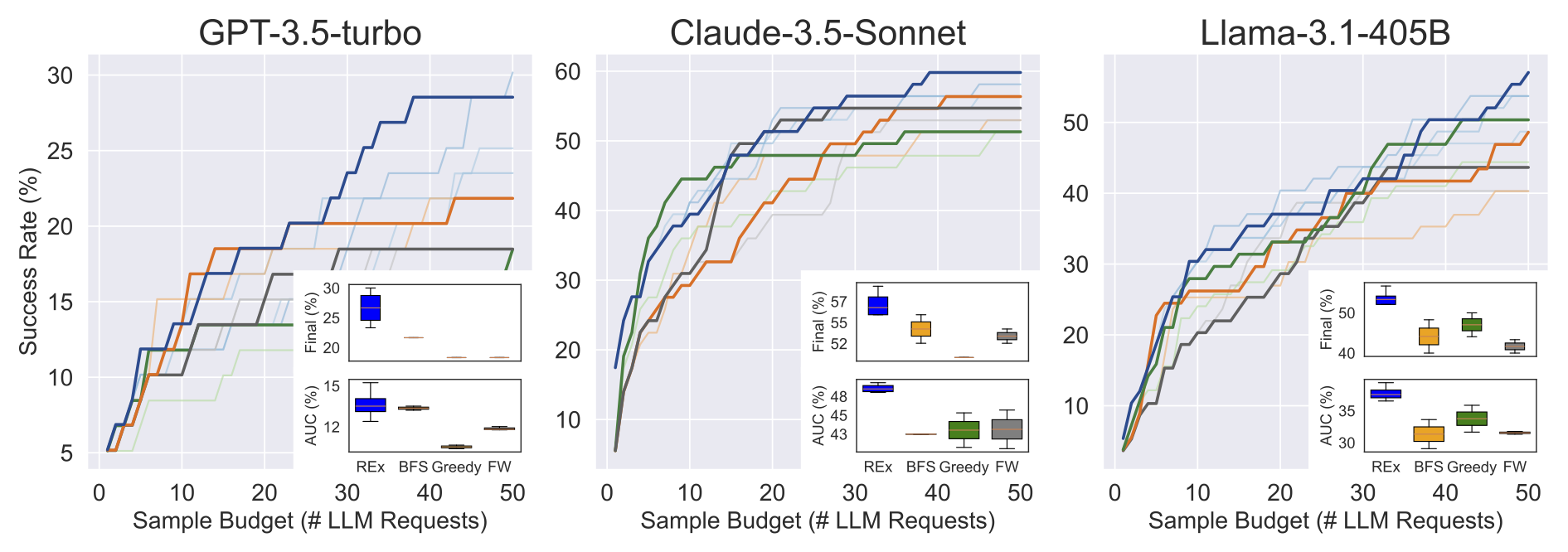
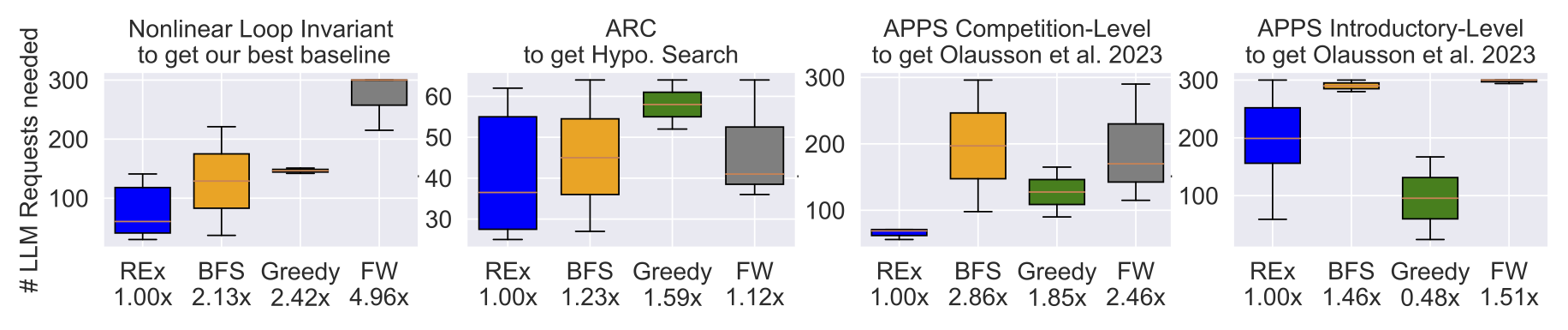
In this work, we demonstrate that code repair with LLMs involves a critical exploration-exploitation tradeoff. Fixed offline refinement strategies are often suboptimal; instead, incorporating dynamic, online guidance is essential for balancing this tradeoff effectively. REx achieves superior performance across three domains and four different LLMs, proving its capability to significantly reduce LLM costs while maintaining high efficiency.
@inproceedings{tang2024code,
author = {Tang, Hao and Hu, Keya and Zhou, Jin Peng and Zhong, Sicheng and Zheng, Wei-Long and Si, Xujie and Ellis, Kevin},
booktitle = {Advances in Neural Information Processing Systems},
title = {Code Repair with LLMs gives an Exploration-Exploitation Tradeoff},
year = {2024}
}